I have been fooling around with Smith Charts lately. They look complicated, but are really pretty easy to understand and use, once you get around all those lines and numbers and stuff. Smith charts offer a great way to visualize what is going on with a particular antenna or transmission line. They can be very useful for AM antenna broadbanding.
.pdf version available here: smith-chart.
The first thing to understand about a Smith chart is normalization. Impedance and reactance are expressed as ratios of value units like VSWR. A ratio of 1:1 is a perfect match. In the center of the Smith chart is point 1, which expresses a perfect match. To normalize, the load resistance and reactance are divided by the input resistance. Thus, if the input resistance is 50 ohms and the load impedance is 50 ohms j0, then the normalized Smith chart point would be 50/50 or 1. If the load impedance is 85 ohms and the reactance is +j60, then the normalized Smith chart point would be .58 1.7,1.2.
More basic Smitch chart usage information in this video:
I touched on the black art of AM antenna broadbanding before. It is a complex topic, especially where directional antenna systems are concerned, as there are several potential bottlenecks in a directional array. To explain this simply, I will use an example of a single-tower non-directional antenna.
Below is a chart of base impedance from a single tower AM antenna on 1430 KHz. The tower is skirted, 125.6 degrees tall. An AM tower that is expressed in electrical degrees is denoting wavelength. A 1/4-wave tower (typical for AM) is 90 degrees tall. A 1/2 wave tower is 180 degrees tall. Thus this tower is slightly taller than 1/4 wavelength.
| Frequnecy(khz) | Reactance | Reactance (normalized) | Resistance | Resistance(normalized) |
| 1390 | -j 139 | -2.78 | 405 | 8.1 |
| 1395 | -j 143 | -2.86 | 400 | 8.0 |
| 1400 | -j 147 | -2.94 | 350 | 7.0 |
| 1405 | -j 146 | -2.92 | 310 | 6.2 |
| 1410 | -j 142 | -2.84 | 270 | 5.4 |
| 1415 | -j 132 | -2.64 | 236 | 4.72 |
| 1420 | -j 125 | -2.50 | 210 | 4.2 |
| 1425 | -j 118 | -2.36 | 190 | 3.8 |
| 1430 | -j 112 | -2.24 | 170 | 3.4 |
| 1435 | -j 106 | -2.12 | 155 | 3.1 |
| 1440 | -j 100 | -2.00 | 138 | 2.76 |
| 1445 | -j 93 | -1.86 | 125 | 2.5 |
| 1450 | -j 86 | -1.72 | 114 | 2.28 |
| 1455 | -j 79 | -1.58 | 104 | 2.08 |
| 1460 | -j 75 | -1.50 | 95 | 1.9 |
| 1465 | -j 70 | -1.4 | 92 | 1.84 |
| 1470 | -j 65 | -1.3 | 85 | 1.7 |
The base impedance is not too far out of line from what is expected for a tower this tall. Plotted on a Smith Chart:
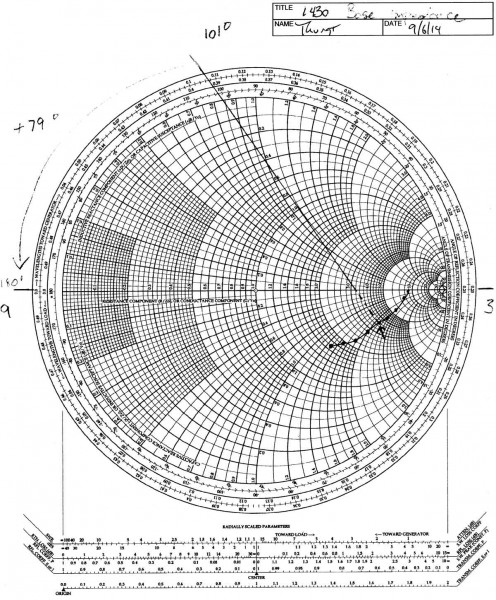
One of the first principles behind broadbanding an AM antenna is to distribute the sideband energy evenly and have a symmetrical VSWR. The antenna tuning unit will match the line impedance to the load impedance and cancel out the reactance. Having the proper phase advance or phase retard rotation will distribute the sideband energy symmetrically about the carrier. To determine phase rotation, the cusp of the plotted graph is rotated to face either the 3 o’clock or 9 o’clock position (0° or 180°). The cusp is where the direction of the line changes, which in this case is the carrier frequency, 1430 KHz. The above example, the line is fairly shallow, which is typical of a skirted tower. Thus, the best phase rotation to start with is +79°. This will likely be close but will need to be tweaked a bit to find the optimum bandwidth. After looking at the plotted Smith chart, my first inclination would be to reduce the rotation, more tower +75° as a first step in tweaking.
When working with AM systems, the bandwidth of the entire system needs to be examined. That means that final bandwidth observations will need to be made at the transmitter output terminal or in some cases, the input to the matching network. It varies on system design, but things like switches, contactors, mating connectors, ATU enclosures, etc can also add VSWR and asymmetry. Broadbanding even a simple one-tower AM antenna can require quite a bit of time and some trial and error.
I will touch on ATU design in the next post.






Zo=50,Zl=85+j60
Normalized 1.7+1.2 no .58+1.2